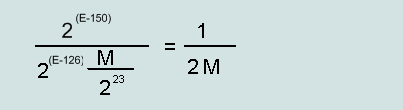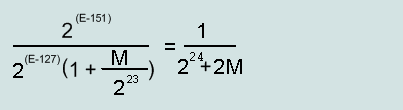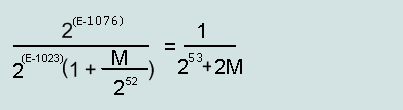Ieee 754 как перевести

Взгляд со стороны: Стандарт IEEE754

1.ЕСТЕСТВЕННАЯ И ЭКСПОНЕНЦИАЛЬНАЯ ФОРМЫ ЗАПИСИ ЧИСЕЛ

Из математики известно, что любое действительное число F в позиционной системе счисления с основанием q записывается на бумаге в виде последовательности цифр. Вес цифры зависит от ее позиции в числе. Основание системы q равно количеству цифр (знаков ее алфавита) и определяет, во сколько раз различаются значения цифр соседних разрядов числа. Такая запись числа называется естественной и выглядит следующим образом:

F = c_(L-1,) c_(L-2)…c_(0.) d_(0 )…d_(N-2,) d_(N-1,) (1)

Где c_(L-1,) c_(L-2)…c_0- цифры целой части, а d_(0 )…d_(N-2,) d_(N-1) — цифры дробной части числа. Число может состоять из сколь угодно большого количества значащих цифр L целой части и N цифр дробной части.
Если точку в числе F, представленном выражением (1) переместить на h разрядов влево, то мы получим новое число М, которое связано с первоначальным числом формулой, представляющей собой экспоненциальную зависимость:

Значение числа F при этом уменьшится в h раз. Чтобы число не изменилось, его умножают на величину q^h. Таким образом, число, записанное в естественном виде (1), может быть представлено в эквивалентном ему экспоненциальном виде:

Если точку в числе F, представленном выражением (1) переместить на h разрядов вправо, то мы получим новое число М, которое связано с первоначальным числом формулой:

Значение числа F при этом увеличится в h раз. Чтобы число не изменилось, его умножают на величину q^(-h). Таким образом, для рассматриваемого случая, число, записанное в естественном виде (1), может быть представлено в следующем эквивалентном ему экспоненциальном виде:

В общем случае, любое действительное число, записанное в естественной форме (1), может быть записано в эквивалентном ему экспоненциальном виде следующим образом:

где М представляет собой число (1) со смещенной точкой на h позиций в ту или иную сторону. Число М в такой записи принято называть мантиссой числа, а q^(±h) характеристикой числа с порядком ±h, который в литературе еще называют экспонентой. Знак и величина порядка h компенсируют величину смещения точки относительно ее первоначального положения в числе (1). Обе записи (1) и (4) суть записи одного и того же числа различным образом.

Число (1) имеет L + N разрядов. Поскольку в естественном представлении числа (1) число разрядов L целой части и N разрядов дробной части могут иметь сколь угодно большое значение, то число M в (2) также может иметь сколь угодно большое количество разрядов. В общем случае, количество разрядов числа М в (2) может быть бесконечным. Например, когда число представляет собой периодическую дробь, или число иррационально. На практике мы имеем дело с ограниченным количеством разрядов для представления действительного числа в естественной форме. Сколько бы разрядов числа мы ни писали справа, рано или поздно мы должны ограничить количество разрядов представляемого числа. Хотя бы потому, что писать будет уже некуда. В результате, число сначала ограничивают, а затем округляют до приемлемой для данной задачи крайней правой цифры. При этом, конечно, теряется точность представления этого числа. Вопросы точности представления чисел в математике мы здесь не затрагиваем. Этому вопросу посвящено огромное число работ. Отметим только, что точность представления числа выбирается в разумных пределах и поэтому действительное число всегда записывается с ограничением разрядности. Тем самым, строго говоря, оно становится рациональным числом. В компьютерной литературе, числа, имеющие дробную часть, принято называть действительными числами. Мы тоже будем придерживаться этой терминологии.

В математике, как правило, к представлению чисел в экспоненциальном виде прибегают тогда, когда число, записанное в естественном виде (1), имеет незначащие нули. Чтобы сократить запись и не писать повторяющиеся незначащие цифры используют запись числа в экспоненциальной форме (2). Тогда порядок характеристики h указывает на количество незначащих нулей до или после точки. В более общем случае, число h со знаком, как мы видели выше, указывает на количество смещений точки относительно ее первоначального положения в числе. В любом случае, когда указывается число сдвигов h, всегда известна и точка отсчета, относительно которой происходит смещение разделительной точки в числе.

2. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В МАШИННОМ СЛОВЕ

В вычислительном устройстве для записи числа отводится ограниченное разрядное пространство. Поэтому на числа, записываемые в машинное слово, накладываются определенные ограничения, которые определяют точность представления чисел и диапазон принимаемых ими значений.

Двоичное число, представленное в экспоненциальном виде, в компьютере записывается в виде машинного слова, разбитого на специальные области. Структура машинного слова может быть схематично представлена следующим образом:

В этом слове К разрядов отводится для записи мантиссы M, R разрядов под запись порядка h характеристики и по одному разряду отводится под запись знака S числа и z знака порядка. Машинное пространство, выделенное под запись мантиссы числа, будем называть областью машинной мантиссы (ОММ), а число, записанное в эту область, машинной мантиссой. Аналогично, пространство, выделенное в машине под запись порядка характеристики, будем называть областью машинного порядка (ОМП) характеристики, а число, записанное в эту область будем называть машинным порядком. Если в ОММ в явном виде содержится точка, то числа, представленные в таком формате, называются числами с фиксированной точкой. Далее мы будем рассматривать числа, записанные в экспоненциальном виде (2). Числа, представленные в таком формате, называют еще числами с плавающей точкой.

3. НОРМАЛИЗАЦИЯ ЧИСЕЛ

Как уже отмечалось выше, при преобразовании числа, записанного в естественном виде, к экспоненциальному виду, точка в числе вида (1) может смещаться на произвольное количество разрядов вправо или влево. А, чтобы значение числа при этом не изменилось, на количество смещений должен быть откорректирован порядок характеристики экспоненциального числа. Очевидно, что при этом возникает множественность представления одного и того же числа, записанного в экспоненциальном виде.

Возьмем двоичное число 0.001001 и запишем его в экспоненциальном виде в машинное слово, в котором ОММ имеет 3 разряда. В том случае, когда предполагается, что машинная мантисса представлена в виде правильной дроби, мы будем иметь следующие возможные варианты записи этого числа: 0.1001•2^(-2)=0.100•2^(-2)=0.010•2^(-1)=0.001•2^0. Во всех этих случаях младший разряд записываемого числа был утерян, поскольку он вышел за пределы разрядной сетки ОММ. Итак, мы получили запись одного и того же числа различными вариантами.

Налицо неоднозначность представления чисел в машинном слове. Мы должны указать машине критерий выбора, по которому отдается предпочтение той или иной форме записи числа в машинном слове. Запись экспоненциального числа в формате, в котором мантисса числа представляется единственным образом, называется нормализацией.

В настоящее время чаще всего рассматриваются два варианта нормализации чисел. В первом варианте [1], перед записью в машинное слово число представляется в виде двоичного дробного числа, в котором единица стоит сразу после точки. При такой нормализации двоичная мантисса в виде правильной дроби лежит в диапазоне 0.1≤М

Источник

Перевод числа в строку с помощью FPU

Введение

Часто требуемое для вывода результатов расчетов преобразование числа с «плавающей точкой» из формата IEEE-754 в текстовую строку в «научной» нотации (т.е. с показателем степени «E») не является совсем уж тривиальной задачей. В силу обстоятельств автору пришлось самостоятельно «изобретать велосипед» такого преобразования. Причем хотелось сделать это максимально эффективно, в полной мере используя аппаратные возможности обработки чисел.

Как ни странно, в литературе мне не попалось ни одного готового примера на эту тему. Поэтому описываемое ниже собственное решение призвано восполнить этот пробел в виде представленной ассемблерной процедуры, которая входит в системную библиотеку сопровождаемого транслятора в течение многих лет и, таким образом, надежно проверена на практике.

Постановка задачи

Формализуем задачу. Необходимо перевести восьмибайтовое число из формата IEEE-754 в текстовую строку, где указан знак числа, мантисса заданной длины и десятичный порядок с признаком «E» и своим знаком.

Так, если задано число 1234.567890, то строка с мантиссой, например, в 16 знаков должна выглядеть как « 1.23456788999999E+003». Вместо плюса у мантиссы нужно писать пробел, а сама мантисса должна быть не меньше единицы. Кстати, данный пример иллюстрирует дискретность и приближенность представления чисел в формате IEEE-754: приведенное исходное число не может быть точно представлено как «1.23456789000000E+003», что, может быть, интуитивно ожидалось.

Использование команд FPU для преобразования

На первый взгляд, решение выглядит простым. В устройстве FPU (Floating Point Unit) процессора даже имеются команды, явно предназначенные и для перевода чисел из формата IEEE-754 в текст. Это, во-первых, команда EXTRACT разделения числа на мантиссу и порядок, а во-вторых, команда FBSTP выдающая мантиссу сразу в виде двоично-десятичного значения. Однако при ближайшем рассмотрении эти команды не дают нужного результата.

Например, если применить команду FBSTP к указанному выше числу, то получится 10 байт со значением 35 12 00 00 00 00 00 00 00 00, поскольку нецелочисленные значения сначала округляются согласно полю RC управляющего слова FPU. Это двухбитовое поле RC может принимать 4 значения, но среди них нет режима «отключить округление». Поэтому часть мантиссы просто теряется, единственное чего можно добиться режимами округления – это еще получить значение 34 12 при округлении к меньшему.

Да и порядок числа, так легко выделяемый командой EXTRACT, является все же степенью двойки, а не десятки, как требуется в данном случае для вывода.

Итак, при использовании возможностей FPU придется решать две задачи.

Во-первых, умножением (или делением) исходного числа на десять нужно «перегнать» всю мантиссу в целочисленную часть числа, тогда команда FBSTP выдаст, наконец, в двоично-десятичном виде все цифры мантиссы.

Во-вторых, нужно определить такой десятичный порядок (опять-таки умножением или делением на десять), при котором результат попадет в диапазон между 1 и 10. Это нужно для представления числа в виде мантиссы с одной цифрой перед точкой и найденным порядком. Увы, совместить эти две задачи в едином цикле умножения/деления невозможно.

Причем есть и «подводный камень» в виде значения числа, максимально приближенного к единице, но не равного единице. Циклом деления или умножения легко можно ошибиться в показателе степени и вместо требуемого в данном случае 9.999…E-001 получить неправильное значение типа 9.999…E+000. К сожалению, при всем богатстве команд FPU обойтись без циклов деления и умножения на десять не удается.

Алгоритм преобразования

При формировании мантиссы для числа типа «double» умножение или деление на 10 продолжаются до тех пор, пока двоичный порядок числа не достигнет (или не станет больше/меньше) 53, поскольку под мантиссу выделено именно 53 двоичных разряда.

Пример реализации преобразования

Далее приведена ассемблерная подпрограмма преобразования числа в текст именно так, как она записана в системной библиотеке. Хотя при этом появляются дополнительные детали, связанные с особенностями использования в конкретном трансляторе, я считаю правильнее ничего не выбрасывать и не превращать реализацию в короткий, но искусственный и не работающий во всех случаях пример.

Пара комментариев к тексту. Подпрограмма написана на языке ассемблера RASM, который имеет некоторые особенности.

В частности здесь используются «временные» метки в виде символа «@». Алгоритм их реализации следующий: транслятор имеет внутренний счетчик меток. Когда метка «@» встречается в команде перехода, к ней автоматически дописывается значение этого счетчика (т.е. реально создаются метки @0000, @0001 и т.д.). Когда встречается символ «@» с двоеточием, к нему также автоматически приписывается значение счетчика и после этого счетчик увеличивается на 1.

Таким образом, получаются метки, на которые можно передавать управление только вперед и использовать многократно, не придумывая для каждой следующей метки новое имя. Поскольку в ассемблере метки часто используются лишь однократно для обхода группы команд, такой прием упрощает написание и анализ программы.

Кроме этого, для команд FPU в RASM не анализируется размер операнда, он имеется прямо в названиях команд в виде значений 16, 32, 64 или 80.

Но вернемся к задаче. Подпрограмме по адресу в EBX передается исходное восьмибайтовое число в формате IEEE-754 и требуемая длина текстовой строки-результата в AL.

В результате работы число записывается в стек в виде текста в «научной» нотации и в AL сохраняется длина этой строки. Другие регистры не сохраняются.

С целью разгрузить конвейеры процессора некоторые команды «рассыпаны» по тексту и не образуют непрерывных логических цепочек, что несколько затрудняет чтение текста. Но таких мест немного. Программа реентерабельна и может быть использована в параллельных вычислениях. При начале работы программы управляющее слово FPU CW=0360.

Сначала в стеке выделяется место для ответа и заполняется «нулевым» шаблоном, т.е. значением « 0.000… E+000».

Затем проверяется знак числа и в зависимости от него формируется мантисса умножением или делением числа на десять.

Командой FBSTP мантисса переписывается в память из FPU в двоично-десятичном виде и ее часть (заданной длины) переносится в ответ.

После этого исходное число опять-таки умножением или делением на десять как можно ближе «подгоняется» к 1, что позволяет вычислить требуемый десятичный порядок, который и записывается на заранее подготовленное в ответе место.

Заключение

Использование команд FPU сделало данную реализацию довольно компактной (326 байт команд) и удовлетворительной по скорости. Например, на компьютере с процессором Intel Core Solo 1.33 GHz сто миллионов преобразований числа 1234.567890 в текст заняли 89 секунд.

Таким образом, скорость работы данной подпрограммы составила 845 преобразований в секунду на каждый мегагерц тактовой частоты процессора. При этом полный отказ от использования команд FPU вряд ли позволит увеличить скорость требуемого преобразования.

Однако эффективность преобразования числа в текст могла бы быть повышена, если бы разработчики FPU предусмотрели режим «без округления» для команды FBSTP. Это позволило бы при применении этой команды для перевода мантиссы в текст избежать циклов умножения и деления на десять лишь только для получения всех значащих цифр.

Источник

Автор: Яшкардин Владимир &nbsp &nbsp
www.softelectro.ru &nbsp &nbsp
Дата: 2009 &nbsp &nbsp &nbsp &nbsp
Редакция: 04.06.2012
info@softelectro.ru

§1. Название стандарта.

Данный стандарт разработан ассоциацией IEEE (Institute of Electrical and Electronics Engineers) и используется для представления действительных чисел (чисел с плавающей точкой) в двоичном коде. Наиболее используемый стандарт для вычислений с плавающей точкой, используется многими микропроцессорами и логическими устройствами, а также программными средствами.

В 2008 года ассоциация IEEE выпустила стандарт IEEE 754-2008, который включил в себя стандарт IEEE 754-1985.

§2.Краткое описание стандарта.

Стандарт содержит 23 страницы текста в 7 секциях и одном приложении: 1.Scope(Область применения) 1.1 Implementation Objectives (Описывает цели стандарта) 1.2 Inclusions (Описывает что включено в стандарт) 1.3 Exclusions (Описывает что не определяет стандарт) 2.Definitions (Вводимы определения) 3.Formats (Форматы чисел) 3.1 Sets of Values (Наборы переменных для представления формата) 3.2 Basic Formats (Базовые форматы) 3.3 Extended Formats (Расширенные форматы) 3.4 Combinations of Formats (Комбинирование форматов) 4.Rounding (Округления) 4.1 Round to Nearest (Округление к ближайшему) 4.2 Directed Roundings (Прямое округление) 4.3 Rounding Precision (Точность округления) 5.Operations (Операции) 5.1 Arithmetic (Арифметика) 5.2 Square Root (Квадратный корень) 5.3 Floating-Point Format Conversions (Конверсия форматов с плавающей точкой) 5.4 Conversion Between Floating-Point and Integer Formats (Конверсия между форматами с плавающими точками и форматами целых чисел.) 5.5 Round Floating-Point Number to Integer Value (округление чисел с плавающей точкой в целые числа) 5.6 Binary Decimal Conversion (Конверсия бинарного в десятичное) 5.7 Comparison (Сравнение) 6.Infinity, NaNs, and Signed Zero (Бесконечность, не числа, и знаковый ноль) 6.1 Infinity Arithmetic (Арифметические действия с бесконечностями) 6.2 Operations with NaNs (Операции с не числами) 6.3 The Sign Bit (Операции с знаковым бит) 7.Exceptions (Исключения) 7.1 Invalid Operation (Недопустимые операции) 7.2 Division by Zero (Деление на ноль) 7.3 Overflow (Переполнение) 7.4 Underflow (Нехватка разряда) 7.5 Inexact (Неточность) 8.Traps (Обнаружение недопустимых операций) 8.1 Trap Handler (Исполнитель обнаружения недопустимых операций) 8.2 Precedence (Первоочередность) A.Recommended Functions and Predicates (Рекомендованные функции и утверждения)

&nbsp &nbsp &nbsp &nbspК сожалению, организация IEEE превратилась из международной общественной инженерной организации (которой она была изначально) в торговую организацию.
Этой организации принадлежит авторское право на публикацию стандарта IEEE754-1985.
Поэтому если вы захотите ознакомиться, с оригиналом стандарта, вам придется купить его примерно за 80$.
Но, Российского законодательство разрешает мне в учебных целях комментировать данный стандарт.
Поэтому дальше я буду давать вольное изложение стандарта и выражать своё мнение о нём в учебных целях.

§3. Основные понятия в представлении чисел с плавающей точкой.

3.1 Представление числа в нормализованном экспоненциальном виде.

3.2 Представление числа в денормализованном экспоненциальном виде.

3.3 Преобразование десятичного числа в двоичное число с плавающей точкой.

Наша задача сводится к представлению десятичного числа с плавающей точкой, в двоичное число с плавающей точкой в экспоненциальном нормализованном виде. Для этого разложим заданное число по двоичным разрядам:

Приведем полученное число к нормализованному виду в десятичной и двоичной системе:
1,55625∙exp₁₀ +2 = 1,0011011101∙exp₂ +111

В результате мы получили основные составляющие экспоненциального нормализованного двоичного числа:
Мантиссу M=1,0011011101
Экспоненту exp 2= +111

§4. Описание преобразования чисел по стандарту IEEE 754.

4.1 Преобразование двоичного нормализованного числа в 32 битный формат IEEE 754

Основное применение в технике и программирование получили форматы 32 и 64 бита.
Например, в VB используют типы данных single (32 бита) и double (64 бита).
В Си аналогично используют float (32 бита) и double (64 бит)
Рассмотрим преобразование двоичного числа 10011011,101 в формат single-precision (32 бита) стандарта IEEE 754.
Остальные форматы представления чисел в IEEE 754 являются увеличенной копией single-precision.

Чтобы представить число в формате single-precision IEEE 754 необходимо привести его к двоичному нормализованному виду. В §3 мы проделали это преобразование над числом 155,625. Теперь рассмотрим, как двоичное нормализованное число преобразуется к 32 битному формату IEEE 754.

В результате десятичное число 155,625 представленное в IEEE 754 c одинарной точностью равно 431BA000 (hex).

4.2 Преобразования числа формата 32 бит IEEE 754 в десятичное число

Это целые числа которые записанные в числе IEEE 754 в двоичном виде.

Приведём формулу для получения десятичного числа из числа IEEE754 одинарной точности:

Проверяем наш пример:
F =(-1) 0 ∙2 (134-127) ∙(1+ 1810432 / 2 23 )= 2 7 ∙(1+0,2158203125)=128∙1,2158203125=155,625

§5. Формальное представление чисел в стандарте IEEE 754 для любого формата точности.

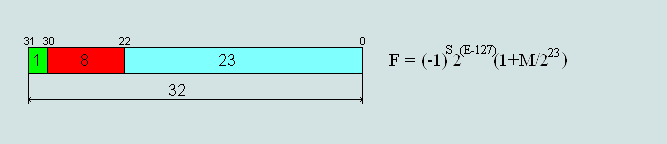
Рис. 1 Представление числа в формате IEEE 754

Формула вычисления десятичных чисел с плавающей точкой, из чисел представленных в стандарте IEEE754:

(Формула №1)

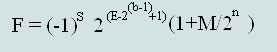
Используя формулу №1 вычислим формулы для нахождения десятичных чисел из форматов одинарной (32 бита) и двойной (64 бита) точности IEEE 754:

Рис.2 Формат числа одинарной точности (single-precision) 32 бита

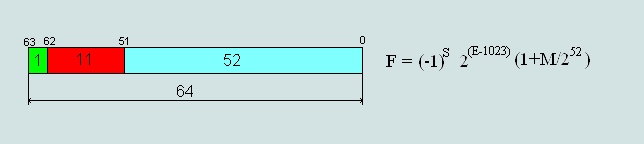
Рис.3 Формат числа двойной точности (double-precision) 64 бита

§6. Представление денормализованного числа и других чисел в формате IEEE 754

Отсюда видно, что невозможно представить число нуль или бесконечность в заданном формате.

Поэтому формула №1 не применяется в следующих случаях:

Формула расчета денормализованных чисел:

(Формула №2)

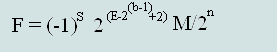
7.2 Полный диапазон чисел одинарной точности (32 бит) по стандарту IEEE754

7.3 Полный диапазон чисел двойной точности (64 бит) по стандарту IEEE754

7.4 Точность представления вещественных чисел в формате IEEE754.

Числа представленные в формате IEEE754 представляют конечное множество, на которое отображается бесконечное множество вещественных чисел. Поэтому исходное число может быть представлено в формате IEEE754 с ошибкой.

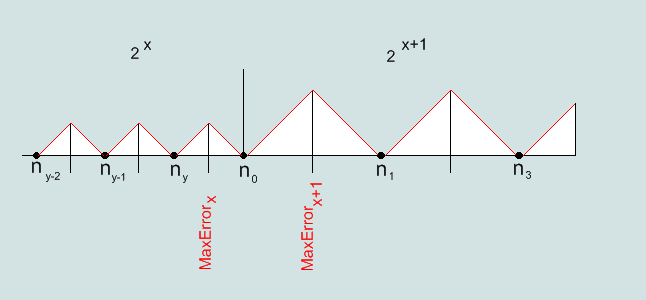
Рис.6 Функция ошибки точности представления числа в IEEE754

Абсолютная максимальная ошибка для числа в формате IEEE754 равна в пределе половине шага чисел. Шаг чисел удваивается с увеличением экспоненты двоичного числа на единицу. То есть, чем дальше от нуля, тем шире шаг чисел в формате IEEE754 по числовой оси.

Шаг денормализованных чисел равен 2 (E-149) (Single) и 2 (E-1074) (Double).
Соответственно предел макс. абсолютной ошибки будет равен 1/2 шага числа: 2 (E-150) (Single) и 2 (E-1075) (Double).
Относительная ошибка в % будет равна: (2 (E-150) /F)*100%(Single) и (2 (E-1075) /F)*100% (Double).

Шаг нормализованных чисел равен 2 (E-150) (Single) и 2 (E-1075) (Double).
Соответственно предел макс. абсолютной ошибки будет равен 1/2 шага числа: 2 (E-151) (Single) и 2 (E-1076) (Double).
Относительная ошибка в % будет равна: (2 (E-151) /F)*100%(Single) и (2 (E-1076) /F)*100% (Double).

Максимальная относительная ошибка для денормализованного числа(single/double):

Максимальная относительная ошибка нормализованного числа(single):

Максимальная относительная ошибка нормализованного числа(double):

7.5 Общие сведенья для чисел одинарной и двойной точности стандарта IEEE 754.

§8. Округление чисел в стандарте IEEE 754.

Стандарт IEEE754 предусматривает четыре способа округления чисел.

§9. Проблемы компьютерных вычислений, вызванные использованием стандарта IEEE754.

Стандарт IEEE 754 широко применяется в технике и программировании.
Большинство современных микропроцессоров изготовляются с аппаратной реализацией представления вещественных переменных в формате IEEE754.
Язык программирования и программист не могут изменить эту ситуацию, иного преставления вещественного числа в микропроцессоре не существует.
Когда создавали стандарт IEEE754-1985 представление вещественной переменной в виде 4 или 8 байт казалось очень большой величиной, так как объём оперативной памяти MS-DOS был равен 1 Мб. А, программа в этой системе могла использовать только 0,64 Мб. Для современных ОС размер в 8 байт является ничтожным, тем не менее переменные в большинстве микропроцессоров продолжают представлять в формате IEEE754-1985.

Рассмотрим ошибки компьютерных вычислений, вызванные применением чисел в формате IEEE754.

9.1 Ошибки связанные с точностью представления вещественных чисел в формате IEEE754. Опасная редукция.

На самом деле ошибки точности представления числа наиболее безобидные в компьютерных вычислениях, и обычно многие программисты на них не обращают никакого внимания. Тем не менее они вас могут сильно огорчить.

9.2 Ошибки связанные с неправильным приведением типов данных. Дикие ошибки.

Эти ошибки вызваны тем, что исходное число представленное в формате single и в формате double обычно не равны друг другу.
Например: исходное число 123456789,123456789
Single: 4CEB79A3=+123456792,0(dec)
Double: 419D6F34547E6B75=+123456789,12345679104328155517578125
Разница между Single и Double составит:2,87654320895671844482421875

Вот пример на VB:
Относительная погрешность результата равна: &#8734 (бесконечности)
Такую ошибку называют «грязным нулем».
Если переменные привести к одному типу, то этой ошибки не будет.
Поэтому переменные и промежуточные результаты компьютерных вычислений должны быть приведены к одному типу данных.
Например, требование приведения данных к одному типу изложено в стандарте на язык Си ISO/IEC 9899:1999.

Обратите внимание на то, что недостаточно просто привести все исходные данные к одному типу. Необходимо привести также результаты промежуточных операций к одному типу.
Вот пример с ошибкой в промежуточном результате:

Здесь ошибка возникает потому, что промежуточный результат 1/3 в строке c=c-1/3 будет иметь тип double, а не single. Чтобы избавиться от ошибки вам надо привести промежуточный результат к типу single с помощью оператора приведения типов CSng. Пример приведения типа данных для GNU C, присланный Григорием Ситкаревым :

Если Вариант 1 (без приведения типов) выполнить с переменными двойной точности (double), то ошибки приведения данных не будет и Result=0.000000
Поэтому в большинстве случаев чтобы избавиться от приведения типов данных надо просто использовать тип данных double и забыть о существовании типа single(float).
Ошибки вычислений вызванные не приведением типов данных я называю «Дикими ошибками», так как они связаны с незнанием стандартов и теории программирования (т.е. с плохим фундаментальным образованием)

9.3 Ошибки вызванные сдвигом мантисс. Циклические дыры.

Эти ошибки связаны с потерей точности результата при неполном пересечении мантисс чисел на числовой оси.
Если мантиссы чисел не пересекаются на числовой оси, то операции сложения и вычитания между этими числами невозможны.
К примеру возьмём число Single: 47FFFFFF = +131071,9921875(dec)
В двоичной системе это число выглядит так: +11111111111111111,1111111

Покажем несколько компьютерных операций сложений и этим числом в формате Single
Значащих цифр в мантиссе двоичного числа в формате Single не более 24
Красным цветом показаны цифры выходящие за этот предел и не участвующие в формате Single

1. сложение с одинаковым числом (ошибка сдвига =0.0).

В последнем примере мантиссы чисел разошлись, и арифметические операции с этими числами становятся бессмысленными.

Как видно из приведенных примеров ошибка сдвига возникает если у исходных нормализованных чисел различаются экспоненты. Если числа отличаются более чем в 2 23 (для single) и 2 52 (для double), то операции сложения и вычитания между этими числами не возможны.
Максимальная относительная погрешность результата операции равна примерно 5,96e-6%, что не превышает относительную погрешность представления числа (см.п.9.1).

Хотя с относительной погрешностью здесь всё в порядке, здесь есть другие проблемы.
Во-первых, работать с числами можно только в узком диапазоне числовой оси, где мантиссы пересекаются.
Во-вторых, для каждого исходного числа существует предел выполнения цикла называемый «Циклической дырой». Поясню, если существует цикл в котором исходное число суммируется к сумме, то существует численный предел суммы для этого числа. То есть сумма достигнув определённой величины перестает увеличиваться от сложения её с исходным числом.

Как вы понимаете, такая система работает в бесконечном цикле.
Допустим в один из дней фасовочная машина простояла слишком долго и бункер заполнился до 300 кг.
Что произойдет после её включения?

Упрощенный пример работы цикла программы управления: В данном примере фасовочная машина забрала из бункера 100 кг продукции, а вес продукции в бункере не изменился.
Почему не изменился?
Потому, что мантиссы чисел 300 и 0,00001 не пересекаются для формата single.

Далее формовочная машина доведет вес бункера до 500 кг и остановится. Фасовочная машина заберет все таблетки из бункера и тоже остановится. Программа будет показывать вес в бункере 500кг. Прибегут специалисты, проверят датчики, провода, компьютер и скажут что программа зависла. Но, программа не зависала, она продолжает работать без сбоев и любой контроль это подтвердит. Просто число 0,0001 попало в циклическую дыру и выйти из него не может.

В результате нам крупно повезло, что это был фармацевтический цех, а не Саяно-Шушенская ГЭС.

На самом деле опытный программист никогда не будет делать циклическое вычитание(или суммирование) таким образом. Этот пример вымышлен специально, и так считать нельзя, хотя с точки зрения математика здесь всё безупречно. Эта ошибка свойственна математикам и начинающим программистам.
Я бы сказал, что основная работа программиста заключается в борьбе с погрешностями, а не в математических решениях поставленной задачи.

Привожу правильный пример решения этой задачи, любезно предоставленный Ситкаревым Григорием: Показанный выше пример взят из реального промышленного кода.
Для наглядности упростим выше приведенный пример.
Как видно из этого примера, программисту приходится вычислять погрешность результата в каждом цикле, чтобы учесть её в следующем цикле.
Обратите внимание, что программист должен быть абсолютно готов к тому, что некоторые основные понятия математики могут не выполняться при вычислениях в формате IEEE754. Например, правила алгебраической коммутативности (a + b) + с = (a + c) + b, обычно не выполняются при таких вычислениях.
К сожалению, в современном фундаментальном математическом образовании этому вопросу уделяют мало внимания, оставляя решения проблем инструментария на прикладного программиста.

9.4 Ошибки вызванные округлением. Грязный ноль.

При компьютерных вычислениях можно выделить два вида округления:
1. Результат выполненной арифметической операции всегда округляется.
2. Вывод и ввод вещественного числа в окно Windows происходит с округлением.

В первом случае переменная округляется по одному из 4-типов округления IEEE754, по умолчанию округление происходит к ближайшему целому.
При этом переменная принимает новое округлённое значение.
В п.9.2 мы рассматривали сложение двух одинаковых чисел:

1. сложение с одинаковым числом (ошибка сдвига =0.0).

Здесь результат операции сложения двух чисел абсолютно точен, но результат был округлен микропроцессором. Таким образом к точному результату была добавлена ошибка округления. В общем случае ошибка округления находится в пределах точности числа.

Во втором случае переменная не меняет своего значения, просто в окно Windows выводится округлённое значение вещественного числа. Получается, что исходная переменная и её отображение в окне Windows это разные числа. Это не ошибка формата IEEE754, это ошибка Windows.
Для переменных типа Single в окне Windows отображается 7 значащих цифр округлённых до ближайшего целого.
3DFCD6EA =+0,12345679104328155517578125 в окне отображается как 0,1234568
Для переменных типа Double в окне Windows отображается 15 значащих цифр округлённых до ближайшего целого.
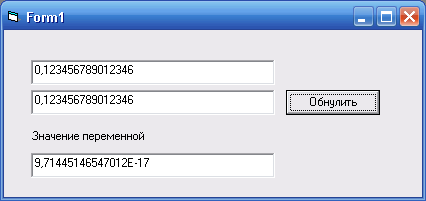
3FBF9ADD3746F67D=+0,12345678901234609370352046653351862914860248565673828125 отображается как 0,123456789012346

Очень часто эта ошибка возникает в интерфейсе «оператор-машина».
Например, при обнулении тары в весовых программах.

Результат выполнения программы приведенного выше примера

9.5 Ошибки на границе норма/денорма числа. Числа убийцы.

Эти ошибки возникают при работе с числами находящимися на границе нормализованного/денормализованного представления чисел. Они связанны с различием в представление чисел в формате IEEE754 и в различии формул перевода формата IEEE754 в вещественные числа. То есть устройства (или программы) должны применять различные алгоритмы в зависимости от положения вещественного числа на числовой оси формата. Кроме того, что это приводит к усложнению устройств и алгоритмов, ещё возникает неопределённость переходной зоны. Неопределённость переходной зоны заключается в том, что стандарт не определяет конкретного значения границы перехода. По сути дела граница перехода находится между двумя вещественными числами:
Последним денормализованным числом 000FFFFFFFFFFFFF:
Точное десятичное значение этого числа:
+2,2250738585072008890245868760858598876504231122409594654935248025624400092282356951787758888037591552642309780950
4343120858773871583572918219930202943792242235598198275012420417889695713117910822610439719796040004548973919380791
9893608152561311337614984204327175103362739154978273159414382813627511383860409424946494228631669542910508020181592
6642134996606517803095075913058719846423906068637102005108723282784678843631944515866135041223479014792369585208321
5976210663754016137365830441936037147783553066828345356340050740730401356029680463759185831631242245215992625464943
0083685186171942241764645513713542013221703137049658321015465406803539741790602258950302350193751977303094576317321
0852507299305089761582519159720757232455434770912461317493580281734466552734375e-308

и первым нормализованным числом 0010000000000000:
Точное десятичное значение этого числа:
+2,2250738585072013830902327173324040642192159804623318305533274168872044348139181958542831590125110205640673397310
3581100515243416155346010885601238537771882113077799353200233047961014744258363607192156504694250373420837525080665
0616658158948720491179968591639648500635908770118304874799780887753749949451580451605050915399856582470818645113537
9358049921159810857660519924333521143523901487956996095912888916029926415110634663133936634775865130293717620473256
3178148566435087212282863764204484681140761391147706280168985324411002416144742161856716615054015428508471675290190
3161322778896729707373123334086988983175067838846926092773977972858659654941091369095406136467568702398678315290680
984617210924625396728515625e-308
Так как граница является вещественным числом, то её точность можно задавать до бесконечности и цифровому устройству или программе может не хватить разрядности для принятия решения к какому диапазону отнести данное число.

§10 Заключение.

Из сказанного выше видно, что мнение о том, что при вычислениях с плавающей точкой результат не выходит за пределы относительной погрешности представления наибольшего числа является ложным. Ошибки перечисленные в п.9 складываются друг с другом. Такие ошибки как грязный ноль и опасная редукция могут сделать погрешность вычислений неприемлемой. Особое внимание при программировании компьютерных вычислений программист должен обратить на результаты близкие к нулю.

Некоторые специалисты считают, что этот формат чисел представляет угрозу человечеству.
Вы можете прочитать об этом в статье IEEE754-тика угрожает человечеству &nbsp
Хотя многие факты из этой статьи излишне драматизированы, и возможно неправильно интерпретированы, но проблема компьютерных вычислений философски отражена правильно.

Я не сторонник драматизации вычислений по стандарту IEEE754. Стандарт работает с 1985 года и полностью вошел в стандарт IEEE754-2008, который расширил точность вычислений. Но, проблема достоверности компьютерных вычислений сегодня очень актуальна, и стандарт IEEE754-2008 и рекомендации ISO не решили эту проблему. Я думаю, в этой области нужна инновационная идея, которой разработчики стандарта IEEE754-2008 к сожалению не обладают.

Если ученые(которые придумывают новое) и специалисты (которые знают как пользоваться известным) не могут решить проблему, то нужна инновация.

Можно представлять вещественные числа, как числа с фиксированной запятой. Для представления всего диапазона чисел Double достаточно иметь переменную состоящую из 1075 битов целой части и 1075 битов дробной части, т.е. около 270 байт на одну переменную. При этом все числа будут представлены с одинаковой абсолютной точностью. Можно работать с числами во всем диапазоне числовой оси, то есть становится возможным суммировать большие числа с малыми числами. Шаг чисел по числовой оси будет равномерен, то есть числовая ось будет линейна. Тип данных будет только один, т.е. не нужны целые, вещественные и др. типы. Здесь возникает проблема реализации регистров микропроцессоров размерностью в 270 байт, но это не проблема для современной технологии.

Для написания п.9 мне пришлось создать программу которая представляет числа в виде переменной с фиксированной точкой, длиною 1075,1075 байтов. Где число можно представить в виде строки символов ASCII, то есть один символ равен одному числовому разряду. Так же пришлось написать все арифметические операции при работе со строками ASCII. Это программа является аналогом бумажного расчета. Так как математические способности микропроцессора в ней не используются, то считает она довольно медленно. Зачем я это сделал?
Я не смог найти программы, которая смогла бы точно представить число формата IEEE754 в десятичном виде.
Так же я не нашел программы (хотя они безусловно есть, в чём нет сомнений) где в окно можно ввести 1075 значащих десятичных цифр.

Вот к примеру точно десятичное значение числа double 7FEFFFFFFFFFFFFF:
+17976931348623157081452742373170435679807056752584499659891747680315726078002853876058955 863276687817154045895351438246423432132688946418276846754670353751698604991057655128207624 549009038932894407586850845513394230458323690322294816580855933212334827479782620414472316 8738177180919299881250404026184124858368,0

Вы можете воспользоваться программой IEEE754 v.1.0 &nbsp
для изучения и оценки погрешностей при работе с вещественными числами представленными в формате IEEE754.

Список литературы:
1. IEEE Standard for Binary Floating-Point Arithmetic. Copyright 1985 by The Institute of Electrical and Electronics Engineers, Inc 345 East 47th Street, New York, NY 10017, USA

Источник